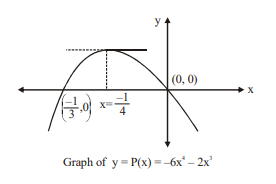
Question

Let $P(x)$ be a biquadratic function of $x$ such that $\operatorname{Lim}_{x \rightarrow 0}\left(\frac{P(-x)}{2 x^3}\right)^{\frac{1}{x}}=\frac{1}{e^3}$.
Which one of the following statement is correct for $P ( x )$ ?

• A. $P ( x )$ has minima but no maxima.
• B. $P ( x )$ has maxima but no minima.
• C. $P ( x )$ increases in $\left(-\infty, \frac{1}{4}\right)$ and decreases in $\left(\frac{1}{4}, \infty\right)$
• D. $P ( x )$ decreases in $\left(-\infty, \frac{-1}{4}\right)$ and increases in $\left(\frac{-1}{4}, \infty\right)$.

Answer 1

Answer: (B)

Let $P ( x )= ax ^4+ bx ^3+ cx ^2+ dx + e$
Now, $ \underset{x \rightarrow 0}{\text{Lim}}\left(\frac{P(-x)}{2 x^3}-1\right) \frac{1}{x}=-3$
$\therefore\underset{x \rightarrow 0}{\text{Lim}}\left(\frac{P(-x)-2 x^3}{x^4}\right)=-6 \Rightarrow \underset{x \rightarrow 0}{\text{Lim}}\left(\frac{a x^4-b x^3+c x^2-d x+e-2 x^3}{x^4}\right)=-6$
So, $e =0, d =0, c =0$
$b+2=0 \text { and } a=-6 \Rightarrow P(x)=-6 x^4-2 x^3$

$P ( x )=-6 x ^4-2 x ^3=-2 x ^3(3 x +1) $
$P ^{\prime}( x )=-24 x ^3-6 x ^2=-6 x ^2(4 x +1)$

So, $P ( x )$ has maxima but no minima.