Question

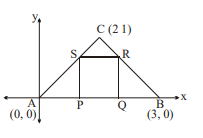
Let $P Q R S$ be a square inscribed in the triangle with vertices $A (0,0), B (3,0)$ and $C (2,1)$. Given that $P , Q$ are on the side $AB , R$ on side $BC$ and $S$ on side $AC$.
The centre of square $PQRS$ is

• A. $\left(\frac{13}{8}, \frac{8}{3}\right)$
• B. $\left(\frac{15}{8}, \frac{3}{8}\right)$
• C. $\left(\frac{15}{8}, \frac{8}{3}\right)$
• D. $\left(\frac{14}{3}, \frac{8}{3}\right)$

Answer 1

Answer: (B)

Let PQRS be the square inscribed in $\triangle ABC$ with length of each side equal to a. Let the coordinates of $P$ be $(p, 0)$. So, the coordinates of $Q , R , S$ are respectively $(p+a, 0),(p+a, a)$ and (p, a).
Now, equation of $AC$ is $y =\frac{1}{2} x$ and $S ( p , a )$ lies on it.
$\Rightarrow a =\frac{ p }{2} \text { or } p =2 a$
Also equation of $BC$ is $( x + y )=3$ and $R ( p + a , a )$ lies on it.

$\therefore(p+a)+a=3 \Rightarrow 4 a=3 \Rightarrow a=\frac{3}{4}$ and $p=\frac{3}{2}$
So, $P \left(\frac{3}{2}, 0\right), Q \left(\frac{9}{4}, 0\right), R \left(\frac{9}{4}, \frac{3}{4}\right)$ and $S \left(\frac{3}{2}, \frac{3}{4}\right)$.
Centre of square PQRS
$=\left(\frac{\frac{3}{2}+\frac{9}{4}}{2}, \frac{0+\frac{3}{4}}{2}\right)=\left(\frac{15}{8}, \frac{3}{8}\right) $