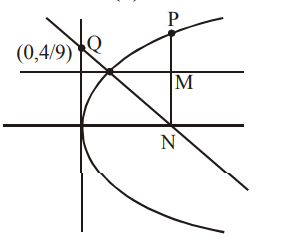
Question

Let $P$ be a point on the parabola, $y^{2}=12 x$ and $N$ be the foot of the perpendicular drawn from $P$ on the axis of the parabola. A line is now drawn through the mid-point $M$ of $PN$, parallel to its axis which meets the parabola at $Q$. If the y-intercept of the line $NQ$ is $\frac{4}{3},$ then

• A. $MQ =\frac{1}{3}$
• B. $PN =3$
• C. $MQ =\frac{1}{4}$
• D. $PN =4$

Answer 1

Answer: (C)

Let $P=\left(3 t^{2}, 6 t\right) ; N=\left(3 t^{2}, 0\right)$
$M =\left(3 t ^{2}, 3 t \right)$
Equation of $MQ : y =3 t$
$\therefore \,\,\,\, Q =\left(\frac{3}{4} t ^{2}, 3 t \right)$
Equation of NQ
$y=\frac{3 t}{\left(\frac{3}{4} t^{2}-3 t^{2}\right)}\left(x-3 t^{2}\right)$
y-intercept of $NQ =4 t =\frac{4}{3} \Rightarrow t =\frac{1}{3}$
$\therefore \,\,\,\, MQ =\frac{9}{4} t ^{2}=\frac{1}{4}$
$PN =6 t =2$