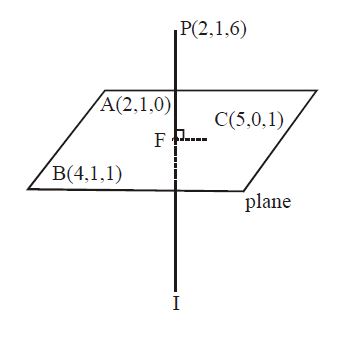
Q. Let P be a plane passing through the points $(2, 1,0), (4 ,1 ,1 )$ and $(5 ,0 ,1 )$ and R be any point $(2,1,6)$. Then the image of R in the plane P is :
Solution:
Plane passing through : $(2, 1, 0), \,(4, 1, 1)$ and $(5, 0, 1)$
$\begin{vmatrix}x-2&y-1&z\\ 2&0&1\\ 3&-1&1\end{vmatrix} = 0$
$\Rightarrow x + y - 2z = 3$
Let I and F are respectively image and foot of perpendicular of point P in the plane.
$eq^{n}$ of line PI $\frac{x-2}{1} = \frac{y-1}{1} = \frac{z-6}{-2} = \lambda \left(say\right)$
Let I $\left(\lambda + 2 , \lambda + 1, -2\lambda + 6\right)$
$\Rightarrow F\left(2+\frac{\lambda }{2},1+\frac{\lambda }{2}, -\lambda +6\right)$
F lies in the plane
$\Rightarrow 2+\frac{\lambda }{2} +\frac{\lambda }{2}+2\lambda -12-3 = 0$
$\Rightarrow \lambda = 4$
$\Rightarrow I \left(6, 5, -2\right)$