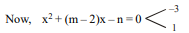Question

Let $\left( p +\frac{1}{ p }\right)\left( q +\frac{1}{ q }\right)\left( r +\frac{1}{ r }\right)< 0$ where $p , q , r \in R -\{0\}$ and $\alpha=\frac{| p |}{ p }+\frac{| q |}{ q }+\frac{| r |}{ r }$. If the equation $x^2+(m-2) x-n=0$ is satisfied by distinct values of ' $\alpha$ ' then find the value of $(m+n)$.

Answer 1

$ \left(p+\frac{1}{p}\right)\left(q+\frac{1}{q}\right)\left(r+\frac{1}{r}\right)<0$
$\Rightarrow p , q , r$ all three are negative or exactly one of then is negative
$\therefore \alpha=-3$ or 1

$ -(m-2)=-2 \Rightarrow m=4 $
$ -n=3 \Rightarrow n=3 $
$\therefore m+n=7 .$