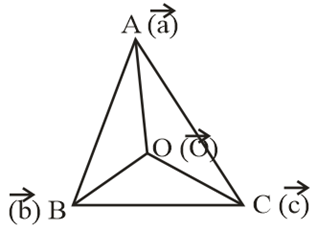
Question

Let $O$ be an interior point of triangle $ABC,$ such that $2\overset{ \rightarrow }{O A}+3\overset{ \rightarrow }{O B}+4\overset{ \rightarrow }{O C}=0,$ then the ratio of the area of $\Delta ABC$ to the area of $\Delta AOC$ is

• A. $3:1$
• B. $3:2$
• C. $2:1$
• D. $4:3$

Answer 1

Answer: (A)

Let position vectors of $O,A,B,C$ are $\overset{ \rightarrow }{O},\overset{ \rightarrow }{a},\overset{ \rightarrow }{b},\overset{ \rightarrow }{c}$ respectively.
$2\overset{ \rightarrow }{O A}+3\overset{ \rightarrow }{O B}+4\overset{ \rightarrow }{O C}=0$
$\Rightarrow 2\overset{ \rightarrow }{a}+3\overset{ \rightarrow }{b}+4\overset{ \rightarrow }{c}=0$
Area of $\Delta AOC=\frac{1}{2}\left|\overset{ \rightarrow }{O A} \times \overset{ \rightarrow }{O C}\right|=\frac{1}{2}\left|\overset{ \rightarrow }{a} \times \overset{ \rightarrow }{c}\right|$
Area of $\Delta ABC=\frac{1}{2}\left|\overset{ \rightarrow }{B A} \times \overset{ \rightarrow }{B C}\right|=\frac{1}{2}\left|\overset{ \rightarrow }{a} \times \overset{ \rightarrow }{b} + \overset{ \rightarrow }{b} \times \overset{ \rightarrow }{c} + \overset{ \rightarrow }{c} \times \overset{ \rightarrow }{a}\right|$
$=\frac{1}{2}\left|\overset{ \rightarrow }{a} \times \left(\frac{- 4 \overset{ \rightarrow }{c} - 2 \overset{ \rightarrow }{a}}{3}\right) + \left(\frac{- 4 \overset{ \rightarrow }{c} - 2 \overset{ \rightarrow }{a}}{3}\right) \times \overset{ \rightarrow }{c} + \overset{ \rightarrow }{c} \times \overset{ \rightarrow }{a}\right|$
$=\frac{1}{2}\left|\frac{4}{3} \overset{ \rightarrow }{c} \times \overset{ \rightarrow }{a} + \frac{2}{3} \overset{ \rightarrow }{c} \times \overset{ \rightarrow }{a} + \overset{ \rightarrow }{c} \times \overset{ \rightarrow }{a}\right|$
$=\frac{3}{2}\left|\right.\overset{ \rightarrow }{c}\times \overset{ \rightarrow }{a}\left|\right.$
$\frac{A r e a o f \Delta A B C}{A r e a o f \Delta A O C}=\frac{3}{1}$