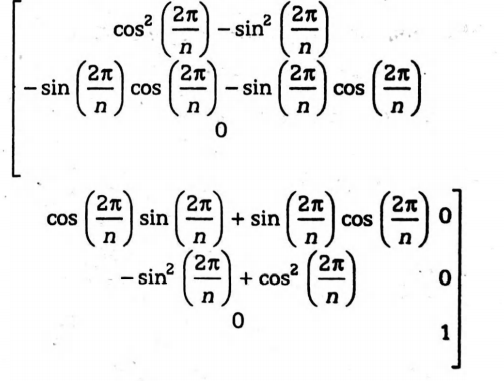Q.
Let $n\ge2$ be an integer,
$A=\begin{pmatrix}\cos\left(2\pi/ n\right)&\sin \left(2\pi / n\right)&0\\ -\sin\left(2\pi / n\right)&\cos\left(2\pi / n\right)&0\\ 0&0&1\end{pmatrix}$
and $Ι$ is the identity matrix of order $3$. Then
Solution: