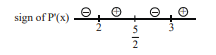Question

Let $\mathrm{P}(\mathrm{x})$ be a polynomial of degree 4 such that $\mathrm{P}(1)=7$ and attains its minimum value 3 at both $x=2$ and $x=3$. If local maximum value of $P(x)$ is $\frac{m}{n}$, where $m \& n$ are relatively prime natural numbers then find the value of $(m-3 n)$.

Answer 1

$\Theta P(x)=a(x-2)^2(x-3)^2+3$
$\therefore P(1)=4 a+3=7 \Rightarrow a=1 $
$\therefore P(x)=(x-2)^2(x-3)^2+3$
$P^{\prime}(x)=2(x-2)(x-3)^2+2(x-2)^2(x-3) $
$=2(x-2)(x-3)(x-3+x-2)$
$=2(x-2)(x-3)(2 x-5)$

$\therefore$ Maximum value of $P ( x )$ occurs at $x =\frac{5}{2}$
$\therefore$ Local maximum value $=3+\frac{1}{16}=\frac{49}{16}$.