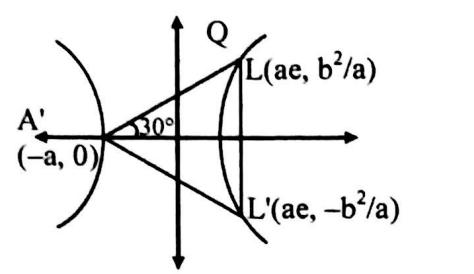
Question

Let $L L^{\prime}$ be the latus rectum through the focus of the hyperbola $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ and $A^{\prime}$ be the farther vertex. If $\triangle A^{\prime} L L^{\prime}$ is equilateral and the eccentricity of the hyperbola (axes are coordinate axes) is $\left(1+\frac{1}{ k }\right)$ then find $k$.

Answer 1

$\tan 30^{\circ}=\frac{\frac{b^{2}}{a}}{a+a e}$
$\Rightarrow \frac{1+e}{\sqrt{3}}=e^{2}-1$
$\Rightarrow e -1=\frac{1}{\sqrt{3}}$
$ \Rightarrow e =\frac{\sqrt{3}+1}{\sqrt{3}}$