Question

Let $L_1$ and $L_2$ denote the lines
$\vec{r}=\hat{i}+\lambda\left(-\hat{i}+2\hat{j}+2\hat{k}\right), \lambda\,\in\,\mathbb{R}$ and
$\vec{r}=\mu\left(2\hat{i}-\hat{j}+2\hat{k}\right), \mu\,\in\,\mathbb{R}$
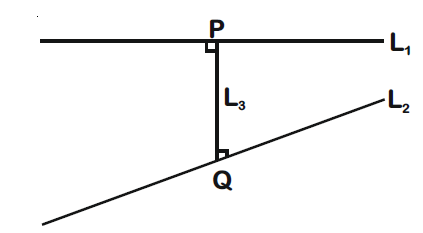
respectively. If $L_3$ is a line which is perpendicular to both $L_1$ and $L_2$ and cuts both of them, then which of the following options describe(s) $L_3$?

• A. $\vec{r}=\frac{2}{9}\left(4\hat{i}+\hat{j}+\hat{k}\right)+t\left(2\hat{i}+2\hat{j}-\hat{k}\right),t\,\in\,\mathbb{R}$
• B. $\vec{r}=\frac{2}{9}\left(2\hat{i}-\hat{j}+\hat2{k}\right)+t\left(2\hat{i}+2\hat{j}-\hat{k}\right),t\,\in\,\mathbb{R}$
• C. $\vec{r}=\frac{1}{3}\left(2\hat{i}+\hat{k}\right)+t\left(2\hat{i}+2\hat{j}-\hat{k}\right),t\,\in\,\mathbb{R}$
• D. $\vec{r}=t\left(2\hat{i}+\hat{j}-\hat{k}\right),t\,\in\,\mathbb{R}$

Answer 1

Answer: (A), (B), (C)

$\because$ $L_3$ is perpendicular to both $L_1$ and $L_2$.
Then a vector along $L_3$ will be,
$\begin{vmatrix}\hat{i}&\hat{j}&\hat{k}\\ -1&2&2\\ 2&-1&2\end{vmatrix}=3\left(2\hat{i}+2\hat{j}-\hat{k}\right)$
Consider a point on $L_{1} as P\left(-\lambda+1,2\lambda,2\mu-2\lambda\right)$ and a point on $L_2$ as $Q\left(2\mu,-\mu, 2\mu\right)$
DR's of $L_{3} <2\mu+\lambda-1, -\mu-2\lambda, 2\mu-2\lambda >$
Here $\frac{2\mu+\lambda-1}{2}=\frac{-\mu-2\lambda}{2}=\frac{2\mu-2\lambda}{-1}$
$\Rightarrow \lambda=\frac{1}{9}$ and $\mu=\frac{2}{9}$
$P\left(\frac{8}{9}, \frac{2}{9}, \frac{2}{9}\right)$ and $Q\left(\frac{4}{9}, -\frac{2}{9}, \frac{4}{9}\right);$ mid-point of $PQ$ is $R\left(\frac{2}{3}, 0, \frac{1}{3}\right)$
Equation of $L_{3} : \vec{r}=\vec{a}+\lambda\left(2\hat{i}+2\hat{j}-\hat{k}\right),$ here $\bar{a}$ is the position vector of any point on $L_{3}$. Possible vector
of $\bar{a}$ are $\left(\frac{8}{9}\hat{i}+\frac{2}{9}\hat{j}+\frac{2}{9}\hat{k}\right)or\left(\frac{4}{9}\hat{i}-\frac{2}{9}\hat{j}+\frac{4}{9}\hat{k}\right)or\left(\frac{2}{3}\hat{i}+\frac{1}{3}\hat{k}\right)$