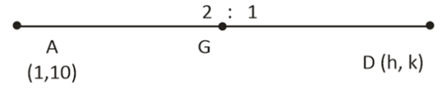
Question

Let in a $\Delta ABC,$ vertex $A,$ the circumcentre $S$ and the orthocentre $H$ are $\left(1 , 10\right), \, \left(- \frac{1}{3} , \frac{2}{3}\right)$ and $\left(\frac{11}{3} , \frac{4}{3}\right)$ respectively, then mid-point of the side $BC$ is

• A. $\left(1 , \frac{- 11}{3}\right)$
• B. $\left(1 , \frac{- 22}{3}\right)$
• C. $\left(2 , \frac{- 11}{3}\right)$
• D. $\left(- 1 , \frac{11}{3}\right)$

Answer 1

Answer: (A)

We know that centroid divides orthocentre and cirumcentre in the ratio $2:1$
Hence, centroid $\left(G\right)$ is $\left(\frac{- \frac{2}{3} + \frac{11}{3}}{3} , \frac{\frac{4}{3} + \frac{4}{3}}{3}\right)$
$\Rightarrow G=\left(1 , \frac{8}{9}\right)$
Let, $D$ is the mid-point of side $BC$ then $G$ also divides $A$ and $D$ in the ratio $2:1$

$\frac{2 h + 1}{3}=1$ and $\frac{2 k + 10}{3}=\frac{8}{9}$
$\Rightarrow h=1$ and $k=-\frac{11}{3}\Rightarrow D=\left(1 , - \frac{11}{3}\right)$