Question

Let for $x \in R$.
$f(x)=\frac{x+|x|}{2} \text { and } g(x)=\begin{cases} x, & x<0 \\ x^2, & x \geq 0 \end{cases}$
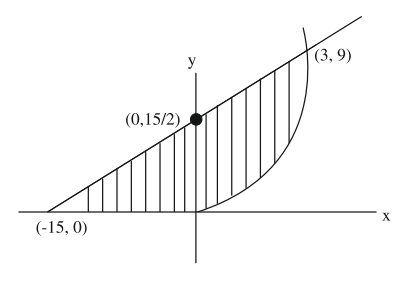
Then area bounded by the curve $y=(f \circ g)(x)$ and the lines $y=0,2 y-x=15$ is equal to

Answer 1

$2 y - x =15$
$A =\int\limits_0^3\left(\frac{ x +15}{2}- x ^2\right) dx +\frac{1}{2} \times \frac{15}{2} \times 15$
$\frac{ x ^2}{4}+\frac{15 x }{2}-\left.\frac{ x ^3}{3}\right|_0 ^3+\frac{225}{4}$
$=\frac{9}{4}+\frac{45}{2}-9+\frac{225}{4}=\frac{99-36+225}{4}$
$=\frac{288}{4}=72$