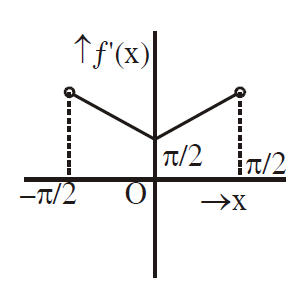Question

Let $f\left(x\right) = xcos^{-1} \left(-sin|x|\right), x \epsilon \left[-\frac{\pi}{2}, \frac{\pi}{2}\right],$ then which of the following is true ?

• A. $f'\left(0\right) = -\frac{\pi}{2}$
• B. f' is decreasing in $\left(-\frac{\pi}{2}, 0\right)$ and mcreasimng in $\left(0, \frac{\pi}{2}\right)$
• C. f is not differentiable at $ x = 0$
• D. f' is increasing in $\left(-\frac{\pi}{2}, 0\right)$ and decreasing in $\left(0, \frac{\pi}{2}\right)$

Answer 1

Answer: (B)

$f (x)$ is an odd function.
Npw, if $x\ge0, f \left(x\right)=xcos^{-1}\left(-sinx\right)$
$=x\left(\frac{\pi}{2}-sin^{-1}\left(-sin\,x\right)\right)=x\left(\frac{\pi}{2}+x\right)$
Hence, $f(x) = \begin{cases} x\left(\frac{\pi}{2}+x\right)\,; & \text{$x\,\in\left[0, \frac{\pi}{2}\right]$} \\[2ex] x\left(\frac{\pi}{2}-x\right)\,; & \text{ $x\,\in- [\frac{\pi}{2}, 0)$ } \end{cases}$
so, $f(x) = \begin{cases} \frac{\pi}{2}+2x\,; & \text{$x\,\in\left[0, \frac{\pi}{2}\right)$} \\[2ex] \frac{\pi}{2}-2x\,; & \text{ $x\,\in (-\frac{\pi}{2}, 0)$ } \end{cases}$