Q.
Let f ( x ) = x sin $\pi$ x , x > 0. Then, for all natural numbers n,
f ( x) vanishes at
Solution:
This equation is based on the concept of transcendal
equation and should be solved with the help of graph.
f (x) = x sin $\pi $ t, t > 0
f (x) = sin $ \pi$ x + $\pi$ x cos $\pi$ x = 0
$\Rightarrow tan \, \pi \, x = - \pi \, x $
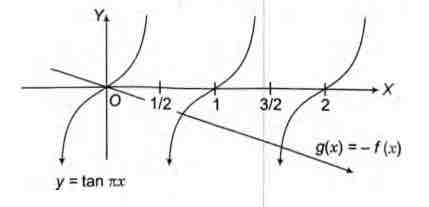
Let f(x) = tan $\pi$ x and g(x) = - $\pi$ x
which could be plotted as,
Clearly, f(x) and g(x) interest when $ \frac{1}{2} < x < 1, $
or $ \frac{3}{2} < x < 2 $
or $ \frac{ 5}{2} < x < 3, $
$\therefore $ A unique point in $ \bigg(n, + \frac{1}{2}, n + 1\bigg)$ or (n, n + 1).