Question

Let $f(x) = x^{4} - 4x^{3} + 4x^{2} +c, c \in \mathbb{R}.$ Then

• A. f(x) has infinitely many zeros in (1, 2) for all c
• B. f(x) has exactly one zero in (1, 2) if -1 < c < 0
• C. f(x) has double zeros in (1, 2) if -1 < c < 0
• D. Whatever be the value of c, f(x) has no zero in (1, 2)

Answer 1

Answer: (B)

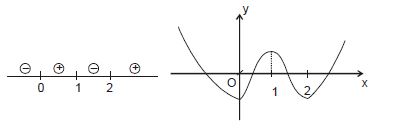
$f\left(x\right) = x^{4} - 4x^{3} + 4x^{2} +c, c \in R$. Then $F'\left(x\right) = 4x^{3} - 12x^{2} + 8x = 4x \left(x^{2} - 3x + 2\right) = 4x\left(x - 1\right) \left(x - 2\right)$
if $-1 < c < 0$
$f\left(1\right) = 1 - 4 + 4 + c$
$= 1 + c > 0$
$f\left(2\right) = 16 - 32 + 16 + c$
$= c < 0$
$f\left(x\right)$ has exactly are zero in $\left(1, 2\right)$ if $-1 < c < 0$