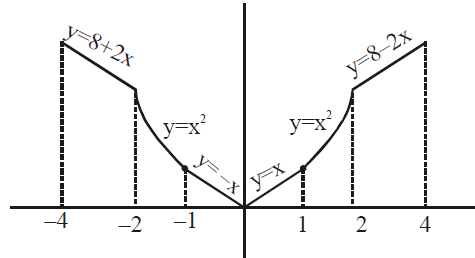
Q.
Let $f(x) = \begin{cases}
\text{max} \{|x| , x^2\}, & |x | \le 2 \\
8 - 2 |x| & 2 < |x| \le 4
\end{cases}
$
Let $S$ be the set of points in the interval $(-4,4)$ at which $f$ is not differentiable. Then $S$:
Solution:
$\begin{cases}
8 + 2x, & -4 \le x < - 2 \\
x^2, & -2 \le x \le - 1 \\
|x|, & -1 < x < 1 \\
x^2 , & 1 \le x \le 2 \\
8 - 2x, & 2 < x \le 4
\end{cases} $
$f( x )$ is not differentiable at $x =\{-2,-1,0,1,2\}$
$
\Rightarrow S =\{-2,-1,0,1,2\}
$