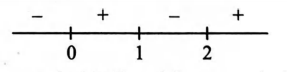Question

Let $f(x)$ be a function defined by
$f(x) = \int\limits_1^x t (t^2 - 3t + 2)dt , 1\le x \le 3$, then the range of $f(x)$ is

• A. $[0, 2]$
• B. $[-\frac{1}{4}, 4]$
• C. $[-\frac{1}{4}, 2]$
• D. None of these

Answer 1

Answer: (C)

Given, $f(x) = \int\limits_1^x t(t^2 - 3t + 2) dt$
$\Rightarrow f'(x) = x(x^2 - 3x + 2) = x(x - 1)(x - 2)$
(using leibnitz rule of derivative)
Now, $f'(x) \le 0$ in $1 \le x \le 2$
$f'(x) \ge 0$ in $2 \le x \le 3$

$\therefore f(x)$ decreases in $[1, 2]$ and increases in $[2, 3]$
$\therefore $ min $(f(x)) = f(2) = \int\limits_1^2 x(x^2 - 3x + 2)dx$
$= (\frac{x^2}{4} - x^3 + x^2) _{1}^{2} = - \frac{1}{4}$
and max $(f(x)) =$ the greatest among $f(1),f(3)$
$\therefore f(1) = \int\limits_1^1 x(x^2 - 3x + 2)dx = 0$
$f(3) = \int\limits_1^3 x(x^2 - 3x + 2)dx= 2$
$\therefore $ max $f(x) = 2$
$\therefore $ range of $f(x) = [ -\frac{1}{4}, 2]$