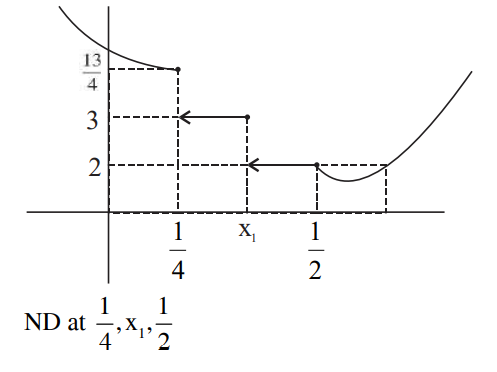
Q.
Let
$f(x)= \begin{cases} \left|4 x^2-8 x+5\right|, \text { if } 8 x^2-6 x+1 \geq 0 \\
{\left[4 x^2-8 x+5\right], \text { if } 8 x^2-6 x+1<0} \end{cases},$
where $[\alpha]$ denotes the greatest integer less than or equal to $\alpha$. Then the number of points in $R$ where $f$ is not differentiable is ______.
Solution:
Correct answer is '3'