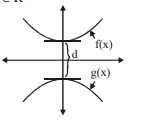
Question

Let $f ( x )=1+3 x ^2+5 x ^4+7 x ^6+\ldots \ldots+21 \cdot x ^{20}, x \in R$ and $g(x)=-x^2+4 \cos ^2 \theta-4 \sin \theta-7, \theta \in R$ If $d$ is the shortest distance between $f ( x ) \& g ( x )$ and $d _1, d _2$ are the least and greatest value of $d$ respectively, then find $\left(\frac{ d _2}{ d _1}\right)$.

Answer 1

$f ( x )=1+3 x ^2+5 x ^4+7 x ^6+\ldots \ldots+21 x ^{20}, x \in R $
$g ( x )=- x ^2+4 \cos ^2 \theta-4 \sin \theta-7, \theta \in R $
$\left. f ( x )\right|_{\min }=1,\left. g ( x )\right|_{\max }=4 \cos ^2 \theta-4 \sin \theta-7 \text { at } x =0$
$\text { shortest distance between } f ( x ) \text { and } g ( x ) \text { is }$
$d =1-\left(4 \cos ^2 \theta-4 \sin \theta-7\right)$
$=1-\left(4-4 \sin ^2 \theta-4 \sin \theta-7\right) $
$=4 \sin ^2 \theta+4 \sin \theta+4$
$=(2 \sin \theta+1)^2+3 $
$d _1=3, d _2=12 $
$\therefore \frac{ d _2}{ d _1}=4 $