Question

Let f : ℝ $/to$ ℝ be given by f(x) = (x - 1)(x - 2)(x - 5). Define
$F\left(x\right) = \int\limits^{x}_{0} f\left(t\right) dt, x > 0.$
Then which of the following options is/are correct?

• A. F has a local minimum at x = 1
• B. F has a local maximum at x = 2
• C. F has two local maxima and one local minimum in (0, $\infty$)
• D. $F\left(x\right) \ne$ 0 for all $x \in \left(0,5\right)$

Answer 1

Answer: (A), (B), (D)

$f(x) = (x - 1) (x - 2) (x - 5)$
$f(x) =$ $\int\limits^{{x}}_{{0}}$ $f(t) dt,x > 0$
$F'\left(x\right)=f\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-5\right), x>0$
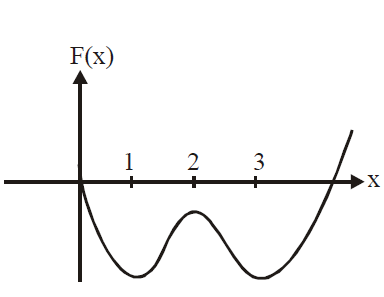
clearly F(x) has local minimum at x = 1,5
$F(x)$ has local maximum at $x = 2$
$f\left(x\right)=x^{3}-8x^{2}+17x-10$
$\Rightarrow F\left(x\right)=$$\int\limits^{{x}}_{{0}}$$\left(t^{3}-8t^{2}+17t-10\right)dt$
$F\left(x\right)=\frac{x^{4}}{4}-\frac{8x^{3}}{3}+\frac{17x^{2}}{2}-10x$
from the graph of $y = F(x)$, clearly $F\left(x\right)\ne0 \forall x\,\in \left(0.5\right)$