Question

Let $f: R \rightarrow R$ be a twice differentiable function such that $f(a)=0, f(b)=2, f(c)=-1, f(d)$ $=2, f ( e )=0$, where $a < b < c < d < c$. Determine the minimum number of zeroes of $g ( x )=\left( f ^{\prime}( x )\right)^2+ f ( x ) \cdot f ^{\prime \prime}( x )$ in the interval $[ a , e ]$.

Answer 1

$ g(x)=\left(f^{\prime}(x)\right)^2+f(x) \cdot f^{\prime \prime}(x)$
$\therefore g ( x ) =\frac{ d }{ dx }\left( f ( x ) \cdot f ^{\prime}( x )\right) $
$f ( a ) = f ( c )=0$
Since $f$ is a continuous function and $f ( b ) \& f ( x )$ have opposite sign $\therefore$ Using IVT $\exists$ atleast one $\alpha$ root in $( b , c )$ similarly $f ( d )$ and $f ( x )$ have opposite sign. $\therefore \exists$ atleast one $\beta$ root in $( c , d )$.
$\therefore f ( x )=0$ has atleast 4 real roots in $[ a , e ]$
Now $f(a)=f(\alpha)=0$ and $f$ is a continuous and derivable function in $[a, \alpha]$
$\therefore $ using Rolle's Theorem $\exists$ atleast some $C _1$ in $[ a , \alpha]$ where $f ^{\prime}\left( c _1\right)=0$
again using Rolle's in $(\alpha, \beta) \exists$ some $c_2$ in $(\alpha, \beta)$ where $f^{\prime}\left(c_2\right)=0 \Rightarrow f^{\prime}(x)$ atleast has 3 real roots.
Using Rolle's in $(\beta, e )$
$\exists$ some $c_3$ in $(\beta, e)$ where $f^{\prime}\left(c_3\right)=0$
$\therefore $ The function $\left.f ^{\prime} x \right) \cdot f ^{\prime}( x )$ has atleast 7 real roots.
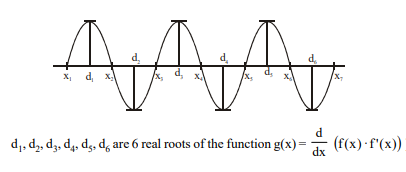
$\therefore g ( x )=\frac{ d }{ dx }\left( f ( x ) \cdot f ^{\prime}( x )\right)$ has atleast 6 real roots.