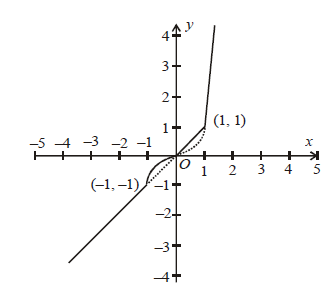Q. Let f : R $\to$ R be a function defined by $f (x) = max \{x, x^3\}$. The set of all points where $f (x)$ is NOT differentiable is
IIT JEEIIT JEE 2001Continuity and Differentiability
Solution:
$f\left(x\right) =\max \left\{ x , x^{3}\right\} = \begin{cases}
x & ; x < - 1 \\
x^3 & ; - 1 \le x \le 0 \\
x & ; 0 \le x \le 1 \\
x^3 & ; x \ge 1
\end{cases} $
$\therefore \ f'(x) = \begin{cases}
1 & ; x < - 1 \\
3x^2 & ; - 1 \le x \le 0 \\
1 & ; 0 \le x \le 1 \\
3x^2 & ; x \ge 1
\end{cases} $
Clearly f is not differentiable at - 1, 0 and 1.
ALTERNATE SOLUTION KEY CONCEPT
A continuous function f (x) is not differentiable at x = a
if graphically it takes a sharp turn at x = a.
Graph of f (x) = max $\{x, x^3\}$ is as shown with solid lines.
From graph of f (x) at x = - 1, 0, 1, we have sharp turns.
$\therefore $ f (x) is not differentiable at x = - 1, 0, 1.