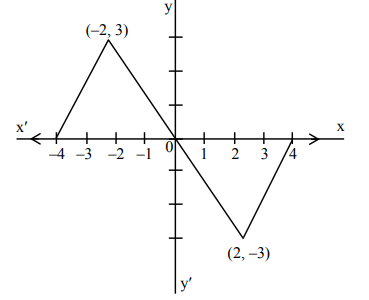Q.
Let $f: R \rightarrow R$ be a function defined
as $f(x)=\begin{cases}3\left(1-\frac{|x|}{2}\right) & \text { if }|x| \leq 2 \\ 0 & \text { if }|x| > 2\end{cases}$
Let $g: R \rightarrow R$ be given by $g(x)=f(x+2)-f(x-2)$.
If $n$ and $m$ denote the number of points in $R$ where $g$ is not continuous and not differentiable, respectively, then $n+m$ is equal to _______.
Solution: