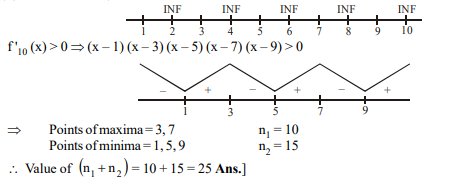
Q. Let $f_N(x)$ be a polynomial function which satisfies $f^{\prime}{ }_N(x)=\prod\limits_{n=1}^N(x-n)^n$. If $n_1$ is sum of values of $x$ for which $f_{10}(x)$ attains maxima and $n_2$ denotes the sum of all values of $x$ for which $f _{10}( x )$ attains minima, then find the value of $\left( n _1+ n _2\right)$.
Application of Derivatives
Solution:
$f _{10}^{\prime}( x )=( x -1)( x -2)^2( x -3)^3 \ldots \ldots( x -10)^{10}$