Q. Let $\frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}=ln\sqrt{\frac{1 + x}{1 - x}}$ , then find $x$ .
NTA AbhyasNTA Abhyas 2022
Solution:
Let $f\left(x\right)=\frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}$
$\Rightarrow y=\frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}$
$\Rightarrow y=\frac{e^{2 x} - 1}{e^{2 x} + 1}$
$\Rightarrow e^{2 x}y+y=e^{2 x}-1$
$e^{2 x}\left(y - 1\right)=-1-y$
$e^{2 x}=\frac{1 + y}{1 - y}$
$e^{x}=\sqrt{\frac{1 + y}{1 - y}}$
$x=ln\sqrt{\frac{1 + y}{1 - y}}$
$f^{- 1}\left(y\right)=ln\sqrt{\frac{1 + y}{1 - y}}$
$f^{- 1}\left(x\right)=ln\sqrt{\frac{1 + x}{1 - x}}$
Now, given equation is
$\frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}=ln\sqrt{\frac{1 + x}{1 - x}}$
$\Rightarrow f\left(x\right)=f^{- 1}\left(x\right)$
The solution of $f\left(x\right)=f^{- 1}\left(x\right)$ is always obtained on $y=x$ line
$\Rightarrow ln\sqrt{\frac{1 + x}{1 - x}}=x$
$\Rightarrow e^{2 x}=\frac{1 + x}{1 - x}$
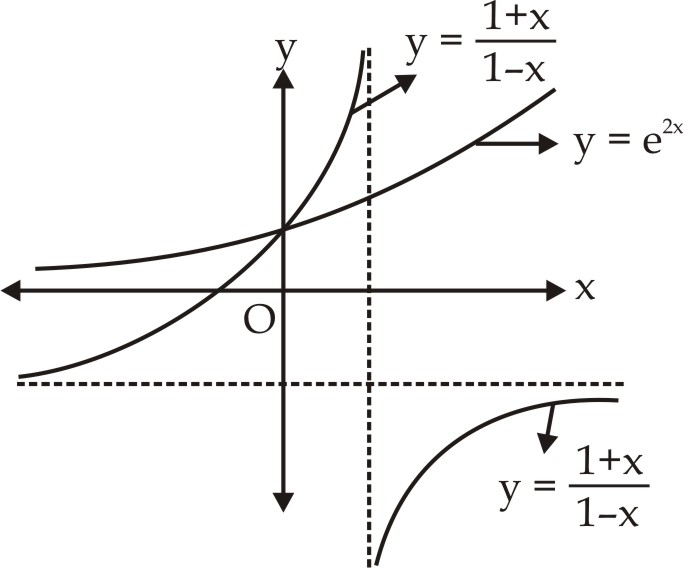
Only one solution $x=0$ .
$\Rightarrow y=\frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}$
$\Rightarrow y=\frac{e^{2 x} - 1}{e^{2 x} + 1}$
$\Rightarrow e^{2 x}y+y=e^{2 x}-1$
$e^{2 x}\left(y - 1\right)=-1-y$
$e^{2 x}=\frac{1 + y}{1 - y}$
$e^{x}=\sqrt{\frac{1 + y}{1 - y}}$
$x=ln\sqrt{\frac{1 + y}{1 - y}}$
$f^{- 1}\left(y\right)=ln\sqrt{\frac{1 + y}{1 - y}}$
$f^{- 1}\left(x\right)=ln\sqrt{\frac{1 + x}{1 - x}}$
$\frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}=ln\sqrt{\frac{1 + x}{1 - x}}$
$\Rightarrow f\left(x\right)=f^{- 1}\left(x\right)$
The solution of $f\left(x\right)=f^{- 1}\left(x\right)$ is always obtained on $y=x$ line
$\Rightarrow ln\sqrt{\frac{1 + x}{1 - x}}=x$
$\Rightarrow e^{2 x}=\frac{1 + x}{1 - x}$

Only one solution $x=0$ .