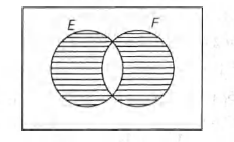
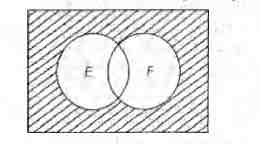
Q. Let $E$ and $F$ be two independent events. The probability that exactly one of them occurs is $\frac{11}{25}$ and the probability of none of them occurring is $\frac{2}{25}$ . If $P(T)$ denotes the probability of occurrence of the event $T$, then
IIT JEEIIT JEE 2011Probability - Part 2
Solution:
$P ( E \cap F ) - P ( E \cap F ) = \frac{11}{25} \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, $...(i)
$ $ [i.e. only E or only F]
'
Neither of them occurs = $\frac{2}{25}$
$\Rightarrow \, \, \, \, \, \, \, \, \, \, \, P(\overline{E} \cap \overline{F})=\frac{2}{25}$ ....(ii)
From Eq. (i), P (E) + P (F ) - 2 P $(E \cap F)=\frac{11}{25} \, \, \, \, \, \, \, \, \, $ ...(iii)
From Eq. (ii), $ \, \, \, \, \, \, \, \, (1-P(E))(1-P(F))=\frac{2}{25}$
$\Rightarrow \, \, \, \, \, \, \, 1-P(E)-P(F)+P(E).P(F)=\frac{2}{25} \, \, \, \, \, $ ..(iv)
From Eqs. (iii) and (iv),
$ \, \, \, \, \, \, \, \, \, \, \, \, P(E) + P(F) = \frac{7}{5} $ and $ P(E).P(F)=\frac{12}{25}$
$\therefore \, \, \, \, \, P(E). \Bigg[\frac{7}{5}-P(E)\Bigg]=\frac{12}{25}$
$\Rightarrow \, \, \, \, \, (P(E))^2-\frac{7}{5} P(E)+\frac{12}{25}=0$
$\Rightarrow \, \, \, \, \bigg[P(E)-\frac{3}{5}\bigg]\bigg[P(E)-\frac{4}{5}\bigg]=0$
$\therefore \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, P(E)=\frac{3}{5} \, or \, \frac{4}{5}$
$\Rightarrow \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, P(F)=\frac{4}{5} \, or \, \frac{3}{5}$