1. Tardigrade
  2. Question
  3. Mathematics
  4. Let d 1(( x 1, y 1),( x 2, y 2))=| x 1- x 2|+| y 1- y 2| and d 2(( x 1, y 1),( x 2, y 2))=√( x 1- x 2)2+( y 1- y 2)2 denote the distance between (x1, y1) and (x2, y2) on the coordinate plane. The area of the region enclosed by the set of points ( x, y) satisfying d1((x, y),(0,0)) ≥ 1 and d2((x, y),(0,0)) ≤ 1, is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

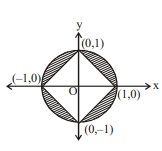
Q. Let $d _1\left(\left( x _1, y _1\right),\left( x _2, y _2\right)\right)=\left| x _1- x _2\right|+\left| y _1- y _2\right|$ and $d _2\left(\left( x _1, y _1\right),\left( x _2, y _2\right)\right)=\sqrt{\left( x _1- x _2\right)^2+\left( y _1- y _2\right)^2}$ denote the distance between $\left(x_1, y_1\right)$ and $\left(x_2, y_2\right)$ on the coordinate plane. The area of the region enclosed by the set of points ( $x, y)$ satisfying $d_1((x, y),(0,0)) \geq 1$ and $d_2((x, y),(0,0)) \leq 1$, is

Application of Integrals

Solution:

Clearly required area $=$ Area of circle - Area of square $=\pi-(\sqrt{2})^2=\pi-2$ (square units)

Solution Image