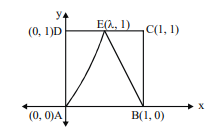
Q. Let $ABCD$ be a square of side 1 unit. A triangle $ABE$ is formed where $E$ is any point on side $C D$. If the greatest possible value of perimeter of triangle $A B E$ is $1+\sqrt{n}$, where $n \in N$, then find the value of $n$.
Application of Derivatives
Solution: