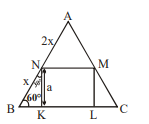
Q. Let ABC be an equilateral triangle and suppose KLMN be a rectangle with K, L on BC, M on AC and N on AB. If AN = 2NB and area of triangle BKN is 6, then area of triangle ABC is equal to
Straight Lines
Solution: