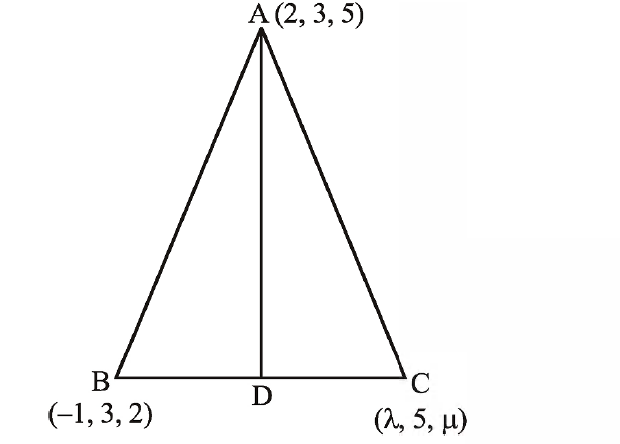
Q. Let $ABC$ be a triangle with vertices at points $A (2, 3, 5), B (-1, 3, 2)$ and $C \left(\lambda, 5, \mu\right)$ in three dimensional space. If the median through A is equally inclined with the axes, then $\left(\lambda, \mu\right)$ is equal to:
Solution:
Since $AD$ is the median
$\therefore D=\left(\frac{\lambda-1}{2} ,4, \frac{\mu+2}{2}\right)$
Now, dR’s of AD is
$a=\left(\frac{\lambda-1}{2}-2\right)=\frac{\lambda-5}{2}$
$b=4-3=1, c=\frac{\mu+2}{2}-5=\frac{\mu-8}{2}$
Also, a, b, c are dR’s
$\therefore a=kl, b =km, c=kn $ where $I = m = n$
and $l^{2}+m^{2}+n^{2}=1$
$\Rightarrow l = m = n =\frac{1}{\sqrt{3}}$
Now, $a = 1,b = 1$ and $c = 1$
$\Rightarrow \lambda=7 \, and \, \mu=10$