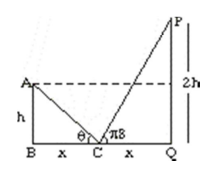
Question

Let $AB$ and $PQ$ be two vertical poles, $160 m$ apart from each other. Let $C$ be the middle point of $B$ and $Q$, which are feet of these two poles. Let $\frac{\pi}{8}$ and $\theta$ be the angles of elevation from $C$ to $P$ and $A$, respectively. If the height of pole $P Q$ is twice the height of pole $AB$, then $\tan ^{2} \theta$ is equal to

• A. $\frac{3-2 \sqrt{2}}{2}$
• B. $\frac{3+\sqrt{2}}{2}$
• C. $\frac{3-2 \sqrt{2}}{4}$
• D. $\frac{3-\sqrt{2}}{4}$

Answer 1

Answer: (C)

Let $BC = CQ = x$ & $AB = h$ and $PQ =2 h$
$\tan \theta=\frac{h}{x}, \tan \frac{\pi}{8}=\frac{2 h}{x}$
$\frac{\tan \theta}{\tan \left(\frac{\pi}{8}\right)}=\frac{1}{2}$
$\tan \theta=\frac{1}{2} \tan \left(\frac{\pi}{8}\right)=\frac{1}{2}(\sqrt{2}-1)$
$\tan ^{2} \theta=\frac{1}{4}(3-2 \sqrt{2})$