1. Tardigrade
  2. Question
  3. Mathematics
  4. Let a function f: (0, ∞) → (0, ∞) be defined by f(x) = | 1 - (1/x) | . Then f is :

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

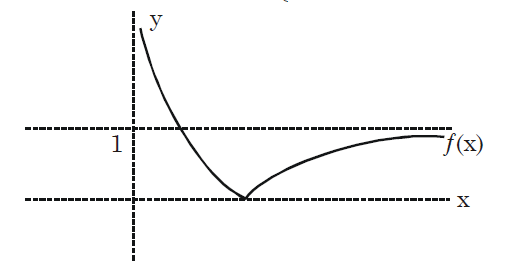
Q. Let a function $f : (0, \infty) \to (0, \infty)$ be defined by $f(x) = | 1 - \frac{1}{x} |$ . Then $f$ is :

JEE MainJEE Main 2019Relations and Functions - Part 2

Solution:

$f\left(x\right) =\left|1- \frac{1}{x}\right| = \frac{\left|x-1\right|}{x} = \begin{cases} \frac{1-x}{x} & 0 < x \le 1 \\ \frac{x-1}{x} & x \ge 1 \end{cases} $
$\Rightarrow \; f(x)$ is not injective
but range of function is $(0, \infty)$
If co-domain is $(0,\infty)$, then $f(x)$ will be surjective

Solution Image