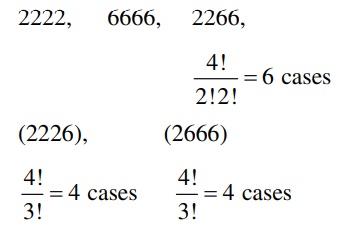Question

Let A denote the set of all $4$ -digit natural numbers with no digit being $0 .$ Let $B \subset A$ consist of all numbers $x$ such that no permutation of the digits of $x$ gives a number that is divisible by $4$ . Then the probability of drawing a number from $B$ with all even digits is

• A. $\frac{625}{1641}$
• B. $\frac{16}{641}$
• C. $\frac{16}{1641}$
• D. $\frac{1000}{1641}$

Answer 1

Answer: (C)

All even digit numbers in $B =\{2,4,6,8\}$ fav : forming a 4 digit nos with all digit is even and not divisible by $4$

Total $=1+1+6+4+4=16$ cases
Total : forming a $4$ -digit no. from $\{1,2, \ldots, 9\}$
but not divisible by $4$
$C-1$ all $4$ digit are add $=5^{4}=625$
$C-2$ all $4$ digit are even $=16$
$C-3$ one even $\& 3$ odd
you can not take $2$ or $6$ as one of even digit $(12,16,32,36, \ldots)$ all are divisible by $4$
But you can take $4$ or $8$ as one of even digit
${ }^{2} C_{1} \times{ }^{4} C_{1} \times 5^{3}=1000$
Take one even digit out of $4 \& 8$
select one place for $4 \& 8$ out of $4$ -places
Total $=1000+625+16=1641$
$P =\frac{\text { fav. }}{\text { total }}=\frac{16}{1641}$