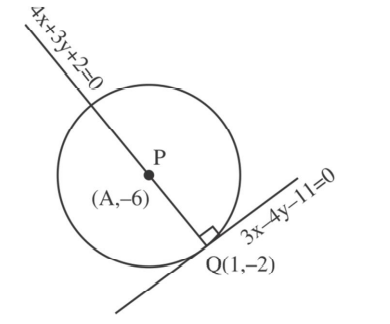
Question

Let a circle $C$ of radius $5$ lie below the $x$-axis. The line $L_{1}=4 x+3 y-2$ passes through the centre $P$ of the circle $C$ and intersects the line $L _{2}: 3 x -4 y -11=0$ at $Q$. The line $L _{2}$ touches $C$ at the point $Q$. Then the distance of $P$ from the line $5 x-12 y+51=0$ is

Answer 1

$4 x+3 y+2=0$
$3 x-4 y-11=0$

$\frac{x}{-25}=\frac{y}{50}=\frac{1}{-25}$
$\frac{x-1}{\cos \theta}=\frac{y+2}{\sin \theta}=\pm 5$
$y=-2+5\left(-\frac{4}{5}\right)=-6$
$x=1+5\left(\frac{3}{5}\right)=4$
Req $\cdot$ distance
$\left|\frac{5(4)-12(-6)+51}{13}\right|$
$=\left|\frac{20+72+51}{13}\right|$
$=\frac{143}{13}=11$