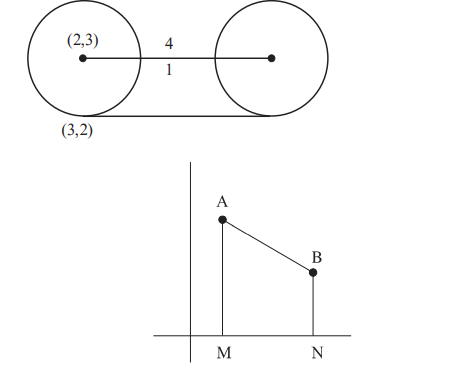
Q. Let a circle $C_1$ be obtained on rolling the circle $x^2+y^2-4 x-6 y+11=0$ upwards 4 units on the tangent $T$ to it at the point $(3,2)$. Let $C_2$ be the image of $C_1$ in $T$. Let $A$ and $B$ be the centers of circles $C_1$ and $C_2$ respectively, and $M$ and $N$ be respectively the feet of perpendiculars drawn from $A$ and $B$ on the $x$-axis. Then the area of the trapezium AMNB is:
Solution:
$C =(2,3), r =\sqrt{2} $
Centre of $G = A =2+4 \frac{1}{\sqrt{2}}, $
$ 3+\frac{4}{\sqrt{2}}=(2+2 \sqrt{2}, 3+2 \sqrt{2})$
$ A (2+2 \sqrt{2}, 3+2 \sqrt{2})$
$B (4+2 \sqrt{2}, 1+2 \sqrt{2})$
$ \frac{ x -(2+2 \sqrt{2})}{1}=\frac{ y -(3+2 \sqrt{2})}{-1}=2 $
$\therefore \text { area of trapezium: } $
$\frac{1}{2}(4+4 \sqrt{2}) 2=4(1+\sqrt{2})$