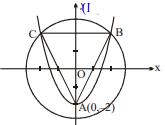
Q. Let $A$ be the vertex of parabola $y = x ^2-2$ and $B , C$ are the intersection points of the parabola with the circle $x^2+y^2=8$. Then the area of triangle $A B C$ is
Conic Sections
Solution:
Solve P & S
$B \equiv(2,2)$
$\therefore (-2,2)$
$\therefore A=\frac{1}{2} \times 4 \times 4=8$