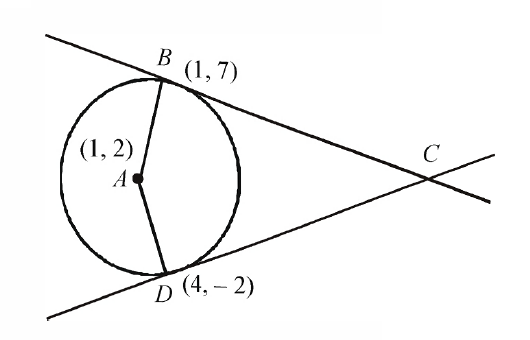
Q. Let $A$ be the center of the circle $x ^{2}+ y ^{2}-2 x -4 y -20=0$, and $B (1,7)$ and $D (4,-2)$ are points on the circle then, if tangents be drawn at $B$ and $D$, which meet at $C$, then area of quadrilateral $ABCD$ is
VITEEEVITEEE 2017
Solution:
$x ^{2}+ y ^{2}-2 x -4 y -20=0$
$A =(1,2)$
Equation of tangent at $B (1,7)$
$x +7 y -( x +1)-2( y +7)-20=0$
$5 y =35$
$y =7$
Equation of tangent at $D (4,-2)$
$4 x -2 y -( x +4)-2( y -2)-20=0$
$3 x -4 y =20$
$\therefore $ coordinates of $C$ are $(16,7)$
Length of $AB =\sqrt{(1-1)^{2}+(7-2)^{2}}=5$
Length of $BC =\sqrt{(16-1)^{2}+(7-7)^{2}}=15$
$\therefore $ The area of quadrilateral
$ABCD =2 \times \frac{1}{2} \times 5 \times 15$
$=75$ sq. units