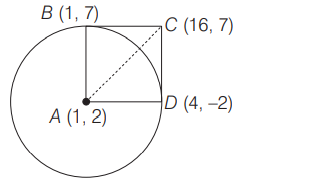
Question

Let $A$ be the centre of the circle $x^{2}+y^{2}-2 x-4 y-20=0$. If the tangents drawn at the point $B(1,7)$ and $D(4,-2)$ on the given circle meet at the point $C$, then the area of the quadrilateral $ABCD$ is

• A. 60
• B. 65
• C. 70
• D. 75

Answer 1

Answer: (D)

Equation of circle
$x^{2}+y^{2}-2 x-4 y-20=0$
Centre of circle $(1,2)$, radius $=5$

Equation of tangents at $(1,7)$ is
$(1) x+7 y-(x+1)-2(y+7)-20=0$
$\Rightarrow \,x+7 y-x-1-2 y+7-20=0$
$ \Rightarrow \,5 y=35$
$\Rightarrow \, y=7\,\,\,\,\,\dots(i)$
Equation of tangent at $(4,-2)$
$4 x-2 y-(x+4)-2(y-2)-20=0$
$\Rightarrow \,4 x-2 y-x-4-2 y+4-20=0$
$\Rightarrow \,3 x-2 y=20 \,\,\,\,\,\,\dots(ii)$
Tangents $y=7$ and $3 x-2 y=20$ intersect at $C$. So, coordinate of $C(16,7)$
Length of $B C=\sqrt{(16-1)^{2}+(7-7)^{2}}$
$BC=15$
Length of $CD=\sqrt{(16-4)^{2}+(7+2)^{2}}=\sqrt{144+81}$
$CD=15$
So, area of $ABCD=$ area of $\Delta \,ABC+$ area of $\Delta \,ACD$
$=\frac{1}{2} \times 15 \times 5+\frac{1}{2} \times 15 \times 5=75$