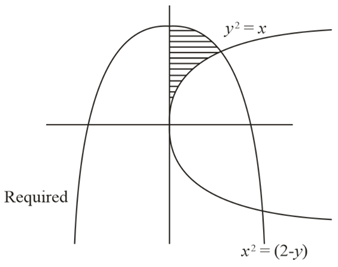
Question

Let $A$ be the area bounded by the curves $y^{2}=4k_{1}x,\forall k_{1}\in \left[\frac{1}{8} , \frac{1}{4}\right]$ , $x^{2}=4k_{2}\left(\right.2-y\left.\right),\forall k_{2}\in \left[\frac{1}{4} , 1\right]$ and $y-$ axis in the first quadrant. Then the least value of $A$ is

Answer 1

The area will be least for maximum $k_{1}$ and minimum $k_{2}$ .

Required area $A=\displaystyle \int _{0}^{1}\left(\left(\right. 2 - x^{2} \left.\right) - \sqrt{x}\right)dx$
$=2-\frac{1}{3}-\frac{2}{3}=2-1=1$ sq. units