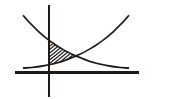
Question

Let ' $a$ ' be a positive constant number. Consider two curves $C_1: y=e^x, C_2: y=e^{a-x}$. Let $S$ be the area of the part surrounding by $C _1, C _2$ and the $y$-axis, then -

• A. $\underset{a \rightarrow-\infty} {\text{Lim}}S=1$
• B. $\underset{a \rightarrow 0}{\text{Lim} }\frac{S}{a^2}=\frac{1}{4}$
• C. Range of $S$ is $[0, \infty)$
• D. S(a) is neither odd nor even

Answer 1

Answer: (A), (B), (C), (D)

$ S =\int\limits_0^{ a / 2}\left(e^{ a - x }-e^{ x }\right) dx $
$=-\left[2 e^{ a / 2}-\left(e^{ a }+1\right)\right]$
Now $\displaystyle\lim _{a \rightarrow 0} \frac{e^a-2 e^{a / 2}+1}{a^2}=\displaystyle\lim _{a \rightarrow 0}\left(\frac{e^{a / 2}-1}{a / 2}\right)^2 \frac{1}{4}=\frac{1}{4}$