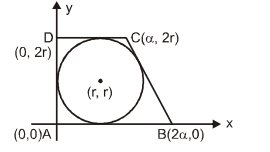
Question

Let $A B C D$ be a quadrilateral with area 18 , with side $A B$ parallel to the side $C D$ and $A B=2 C D$. Let $A D$ be perpendicular to $A B$ and $C D$. If a circle is drawn inside the quadrilateral $A B C D$ touching all the sides, then its radius is

• A. 3
• B. 2
• C. $3 / 2$
• D. 1

Answer 1

Answer: (B)

$18=\frac{1}{2}(3 \alpha)(2 r) \alpha r=6$

Line, $y=-\frac{2 r}{\alpha}(x-2 \alpha)$ is tangent to circle
$ (x-r)^2+(y-r)^2=r^2$
$ 2 \alpha=3 r $ and $ \alpha r=6$
$ r=2$