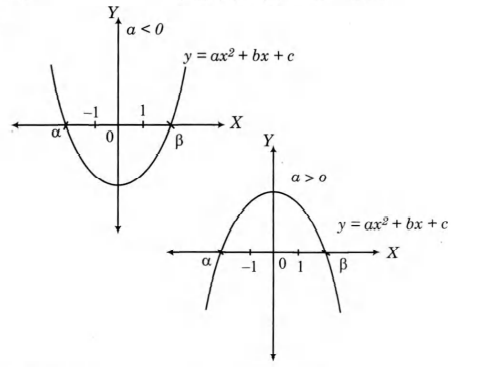
Question

Let $a, b, c$ be real. If $ ax^2 + bx + c = 0$ has two real roots $\alpha$ and $ \beta$ , where $\alpha < - 1 \,$ and $\, \beta > 1$ , then show that $1 + \frac{c}{a} + \bigg | \frac{ b}{a} \bigg | < 0 $

Answer 1

From figure, it is clear that, if $a > 0$, then $f(-1) < 0$ and $f(1) < 0$ and if $a < 0, f(-1) > 0$ and $f(1) > 0$. In both cases, $a f(-1) < 0$ and $a f(1) < 0$.
$\Rightarrow a(a-b+c) < 0 $ and $ a(a+b+c) < 0$
On dividing by $a^{2}$, we get
$1-\frac{b}{a}+\frac{c}{a} < 0 $ and $ 1+\frac{b}{a}+\frac{c}{a} < 0$
On combining both, we get
$1 \pm \frac{b}{a}+\frac{c}{a} < 0 \Rightarrow 1+\left|\frac{b}{a}\right|+\frac{c}{a}<0$