1. Tardigrade
  2. Question
  3. Mathematics
  4. Let A and B be two sets and n(A)=4 and n(B)=2. If number of onto functions from A to B is p and number of one-one functions from B to A is q then (p+q) equals

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

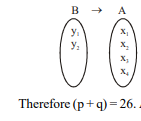
Q. Let $A$ and $B$ be two sets and $n(A)=4$ and $n(B)=2$. If number of onto functions from $A$ to $B$ is $p$ and number of one-one functions from $B$ to $A$ is $q$ then $(p+q)$ equals

Relations and Functions - Part 2

Solution:

Number of onto function from A to B is $=2^4-2 \Rightarrow p=14$
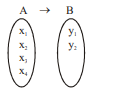
image
Number of one-one function from B to A is, $q=4 \times 3=12$
Aliter :
$q ={ }^4 C _2 \times C _2$
$ =6 \times 2=12$

Solution Image