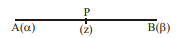Question

Let $A$ and $B$ be two distinct points denoting the complex numbers $\alpha$ and $\beta$ respectively. A complex number $z$ lies between $A$ and $B$ where $z \neq \alpha, z \neq \beta$. Which of the following relation(s) hold good?

• A. $|\alpha- z |+| z -\beta|=|\alpha-\beta|$
• B. $ \exists$ a positive real number ' $t$ ' such that $z =(1-t) \alpha+t \beta$
• C. $\begin{vmatrix} z -\alpha & \overline{ z }-\bar{\alpha} \\ \beta-\alpha & \bar{\beta}-\bar{\alpha} \end{vmatrix}=0 $
• D. $\begin{vmatrix} z & \overline{ z } & 1 \\ \alpha & \bar{\alpha} & 1 \\ \beta & \bar{\beta} & 1 \end{vmatrix}=0$

Answer 1

Answer: (A), (B), (C), (D)

$AP + PB = AB$
$| z -\alpha|+|\beta- z |=|\beta-\alpha| \Rightarrow \text { A True } \\
\text { Now } z =\alpha+ t (\beta-\alpha) $
$=(1- t ) \alpha+ t \beta \text { where } t \in(0,1) \Rightarrow B \text { is True } $
$\text { again } \frac{ z -\alpha}{\beta-\alpha} \text { is real } \Rightarrow \frac{ z -\alpha}{\beta-\alpha}=\frac{\overline{ z }-\bar{\alpha}}{\bar{\beta}-\bar{\alpha}}$
$\Rightarrow\begin{vmatrix}z-\alpha & \bar{z}-\bar{\alpha} \\ \beta-\alpha & \bar{\beta}-\bar{\alpha}\end{vmatrix}=0$
$ \text { also }\begin{vmatrix}z & \bar{z} & 1 \\ \alpha & \bar{\alpha} & 1 \\ \beta & \bar{\beta} & 1\end{vmatrix}=0 \text { if and only if }\begin{vmatrix}z-\alpha & \bar{z}-\bar{\alpha} & 0 \\ \alpha & \bar{\alpha} & 1 \\ \beta-\alpha & \bar{\beta}-\bar{\alpha} & 0\end{vmatrix}=0 $
$\Rightarrow \begin{vmatrix}z-\alpha) & \bar{z}-\bar{\alpha} \\ \beta-\bar{\alpha} & \bar{\beta}-\bar{\alpha}\end{vmatrix}=0$