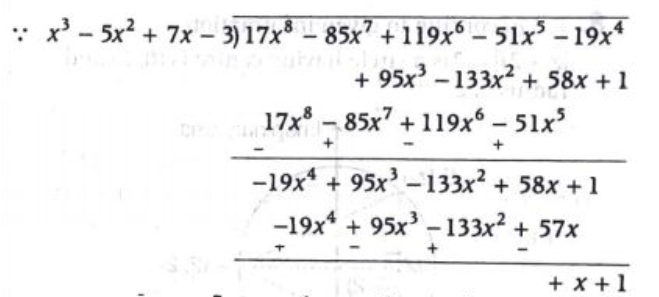Question

Let $[ A ]_{3 \times 3}$ be a non-singular matrix such that $A ^{-1}=\frac{1}{3}\left( A ^{2}-5 A +7 I \right)$ Then $17 A ^{8}-85 A ^{7}+119 A ^{6}-51 A ^{5}-19 A ^{4}+95 A ^{3}-113 A ^{2}+58 A + I =$

• A. $0$
• B. $A$
• C. $A + I$
• D. $A^{2}+A+I$

Answer 1

Answer: (C)

For a non-singular matrix $A_{3 \times 3}$, it is given that
$A^{-1}=\frac{1}{3}\left(A^{2}-5 A+7 I\right) $
$\Rightarrow A^{3}-5 A^{2}+7 A-3 I=0 \ldots $ (i)
$17 x^{5}-19 x$

$\therefore 17 A^{8}-85 A^{7}+119 A^{6}-51 A^{5}-19 A^{4}-133 A^{2}+58 A+I$
$=\left(A^{3}-5 A^{2}+7 A-3 I\right)\left(17 A^{5}-19 A\right)+A+I$
$=A+I \left\{\because A^{3}-5 A^{2}+7 A-3 I=0\right\}$