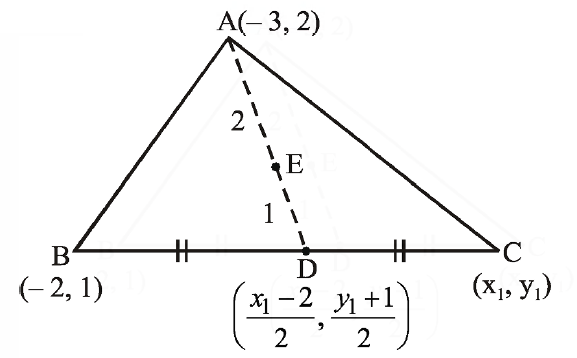
Q. Let $A (-3,2)$ and $B (-2,1)$ be the vertices of a triangle $ABC$. If the centroid of this triangle lies on the line $3x + 4y+2 = 0$, then the vertex $C$ lies on the line :
Solution:
$Let \, C=\left(x_{1}, y_{1}\right)$
Centroid, E=$\left(\frac{x_{1}-5}{3}, \frac{y_{1}+3}{3}\right)$
Since centroid lies on the line
3x + 4y + 2 = 0
$\therefore \, 3\left(\frac{x_{1}-5}{3}\right) +4 \left(\frac{y_{1}+3}{3}\right)+2=0$
$\Rightarrow 3x_{1}+4y_{1}+3=0$
Hence vertex ($x_{1}, y_{1}$) lies on the line
$3x + 4y + 3 = 0$