1. Tardigrade
  2. Question
  3. Mathematics
  4. Let A (1, k), B(1, 1) and C (2, 1) be the vertices of a right angled triangle with AC as its hypotenuse. If the area of the triangle is 1square unit, then the set of values which 'k' can take is given by

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

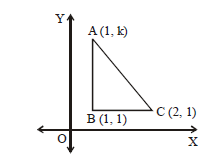
Q. Let A (1, k), B(1, 1) and C (2, 1) be the vertices of a right angled triangle with AC as its hypotenuse. If the area of the triangle is 1square unit, then the set of values which 'k' can take is given by

Straight Lines

Solution:

Given : The vertices of a right angled triangle A(l, k), B(1, 1) and C(2, 1) and Area of $\Delta$ABC = 1 square unit
We know that, area of right angled triangle
$= \frac{ 1}{2} \times BC \times AB = 1 = \frac{1}{2}\left(1\right)\left|\left(k-1\right)\right| $
$ \Rightarrow \pm\left(k-1\right) = 2 \Rightarrow k = - 1, 3 $

Solution Image