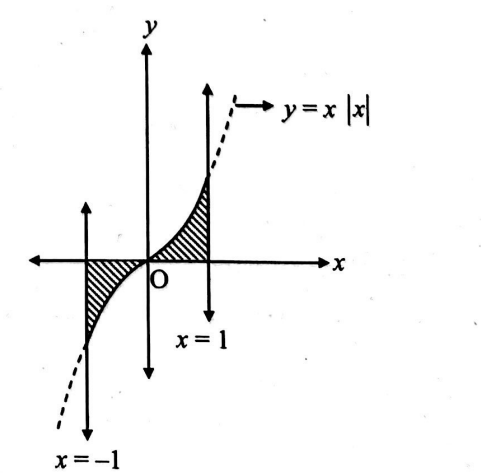
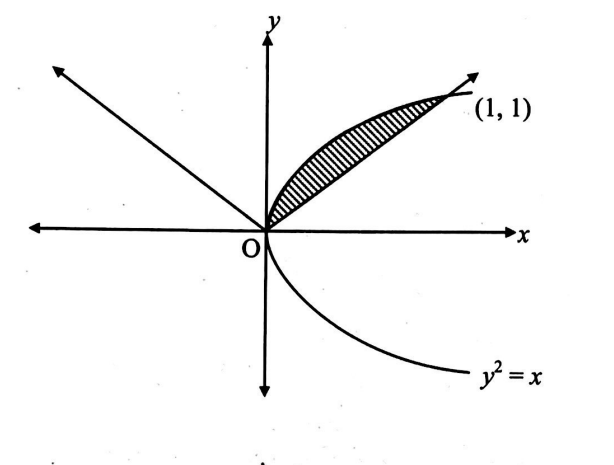
Question

Let $A_{1}, A_{2}$ denote the area bounded by the curve $y=x|x|, x$ axis, the ordinates $x=-1, x=1$ and the area enclosed between the curves $y^{2}=x$, $y=|x| .$ Find $\frac{ A _{1}}{ A _{2}}$.

Answer 1

$A _{1}=2 \int\limits_{0}^{1} x^{2} d x=2\left(\frac{x^{3}}{3}\right)_{0}^{1}=\frac{2}{3}$
$A _{2}=\int\limits_{0}^{1}(\sqrt{x}-x) d x=\left(\frac{2}{3} x^{\frac{3}{2}}-\frac{x^{2}}{2}\right)_{0}^{1}=\frac{2}{3}-\frac{1}{2}$
$=\frac{4-3}{6}=\frac{1}{6}$
$\Rightarrow \frac{A_{1}}{A_{2}}=\frac{\left(\frac{2}{3}\right)}{\left(\frac{1}{6}\right)}=\frac{6 \times 2}{3}=4$