Question

Let $A_1 ,A_2, A_n$ be the vertices of an n-sided regular
polygon such that $ \frac{1}{ A_1 \, A_2 } = \frac{1}{ A_1 \, A_3 } + \frac{1}{ A_1 \, A_4 } .$ Find the value of n.

Answer 1

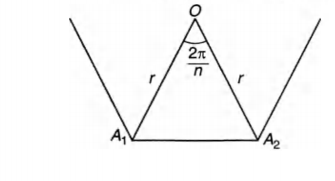
Let O be the centre and r be the radius of the circle
passing through the vertices t $A_1 ,A_2, A_n$ ,
Then, $ \angle A_1 O A_2 = \frac{2 \pi}{n}, \, also \, OA_1 = OA_2 = r $
Again, by cos formula, we know that,
cos $ \bigg( \frac{ 2 \pi}{ n }\bigg) = \frac{ OA_1^2 + OA_2^2 - A_1 \, A_2^2 }{ 2 (OA_1) \, (OA_2) } $
$\Rightarrow cos \bigg( \frac{ 2 \pi}{ n }\bigg) = \frac{ r^2 + r^2 - A_1 \, A_2^2 }{ 2 (r) (r)}$
$\Rightarrow 2r^2 cos \bigg( \frac{ 2 \pi}{ n }\bigg) = 2r^2 - A_1 \, A_2^2 $
$\Rightarrow A_1 \, A_2^2 = 2r^2 - 2r^2 cos \bigg( \frac{ 2 \pi}{ n }\bigg) $
$\Rightarrow A_1 A_2^2 = 2r^2 \bigg [ 1 - cos \bigg( \frac{ 2 \pi}{ n }\bigg) \bigg]$
$\Rightarrow A_1 \, A_2^2 = 2r^2 . 2 \, sin^2 \bigg( \frac{ \pi}{ n }\bigg) $
$\Rightarrow A_1 \, A_2^2 = 4r^2 sin^2 \bigg( \frac{ \pi}{ n }\bigg) $
$\Rightarrow A_1 A_2 = 2r \, sin \bigg( \frac{ \pi}{ n }\bigg) $
Similarly, $ A_1 A_3 = 2r \, sin \bigg( \frac{ 2 \pi}{ n }\bigg) $
and $ A_1 A_4 = 3r \, sin \bigg( \frac{3 \pi}{ n }\bigg) $
Since, $ \frac{1}{ A_1 \, A_2 } = \frac{1}{ A_1 \, A_3 } + \frac{1}{ A_1 \, A_4 } .$ [given]
$\Rightarrow \frac{1}{ 2r \, sin \, (\pi / n)} = \frac{1}{ 2r \, sin \, (2\pi / n)} + \frac{1}{ 2r \, sin \, (3\pi / n)} $
$\Rightarrow \frac{1}{sin \, (\pi / n} = \frac{1}{sin \, (2\pi / n} + \frac{1}{sin \, (3\pi / n} $
$\Rightarrow \frac{1}{sin \, (\pi / n} = \frac{ sin \, \bigg( \frac{3 \pi}{n} \bigg) + sin \bigg( \frac{2 \pi}{n} \bigg) }{ sin \, (2 \pi / n) \, (sin \, (3 \pi / n)} $
$\Rightarrow sin \, \bigg( \frac{2 \pi}{n} \bigg) . sin \bigg( \frac{3 \pi}{n} \bigg) = sin \bigg( \frac{ \pi}{n} \bigg) sin \bigg( \frac{3 \pi}{n} \bigg) + sin \bigg( \frac{ \pi}{n} \bigg) . sin \bigg( \frac{2 \pi}{n} \bigg) $
$\Rightarrow sin \bigg( \frac{2 \pi}{n} \bigg) \bigg [ sin \bigg( \frac{3 \pi}{n} \bigg) - sin \bigg( \frac{ \pi}{n} \bigg) \bigg ] = sin \bigg( \frac{ \pi}{n} \bigg) .sin \bigg( \frac{3 \pi}{n} \bigg) $
$\Rightarrow sin \bigg( \frac{2 \pi}{n} \bigg) \bigg [ \bigg \{ 2 \, cos \, \bigg( \frac{3 \pi + \pi}{2n} \bigg) sin \bigg( \frac{3 \pi - \pi }{2n} \bigg) \bigg \} \bigg ] = sin \bigg( \frac{ \pi}{n} \bigg) . sin \bigg( \frac{3\pi}{n} \bigg)$
$\Rightarrow 2 \, sin \, \bigg( \frac{2 \pi}{n} \bigg) . cos \bigg( \frac{2 \pi}{n} \bigg). sin \bigg( \frac{ \pi}{n} \bigg) = sin \bigg( \frac{ \pi}{n} \bigg) sin \bigg( \frac{3 \pi}{n} \bigg) $
$\Rightarrow 2 sin \bigg( \frac{2 \pi}{n} \bigg) cos \bigg( \frac{2 \pi}{n} \bigg) = sin \bigg( \frac{3 \pi}{n} \bigg) $
$\Rightarrow sin \bigg( \frac{4 \pi}{n} \bigg) = sin \bigg( \frac{3 \pi}{n} \bigg) $
$\Rightarrow \frac{ 4 \pi}{ n } = \pi - \frac{ 3 \pi}{n} $
$\Rightarrow \frac{ 7 \pi}{ n } = \pi$
$\Rightarrow n = 7$.