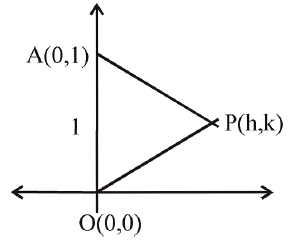
Q. Let $O(0, 0)$ and $A(0, 1)$ be two fixed points. Then the locus of a point $P$ such that the perimeter of $\Delta AOP$ is $4$, is :
Solution:
$AP+OP+AO=4 $
$ \sqrt{h^{2} + \left(k-1\right)^{2}} + \sqrt{h^{2} +k^{2}} + 1 = 4 $
$ \sqrt{h^{2}+\left(k-1\right)^{2}} + \sqrt{h^{2}+k^{2}} = 3$
$ h^{2} +\left(k-1\right)^{2}=9 +h^{2}+k^{2}-6\sqrt{h^{2}+k^{2}} $
$ - 2k - 8 = - 6 \sqrt{h^{2} +k^{2}} $
$ k+4 = 3 \sqrt{h^{2} +k^{2}} $
$ k^{2} +16+8k = 9\left(h^{2} + k^{2}\right) $
$ 9h^{2} +8k^{2} -8k - 16 = 0 $
Locus of P is $ 9x^{2} + 8y^{2} - 8y -16 = 0$